What is a Transformer? | Working Principle | EMF Equation
What is a Transformer?
A transformer may be defined as a static electrical device that transfers electrical energy from one circuit to another circuit at the same frequency but with changed voltage (or current or both) through a magnetic circuit.
Type of Transformer
Transformers are used in various fields such as power generation grid, distribution sector, transmission, and consumption of electric power.
There are several types of transformers that are classified based on the following factors:
- Working voltage range
- The medium used in the core.
- Winding arrangement
- Installation location
Based on voltage levels
The types of transformers in common use, according to the voltage, are classified as follows:
- Step Up Transformer: They are used between the power generator and the electrical network. The secondary output voltage is higher than the input voltage.
- Step Down Transformer – These transformers are used to convert the high-voltage primary supply to a low-voltage secondary output.
Based on the Medium of Core Used
In a transformer, we will find different types of cores that are used.
- Air Core Transformer: The flux link between the primary and secondary winding is through the air. The coil or windings wound on the non-magnetic strip.
- Iron Core Transformer – The windings are wound on multiple iron plates stacked together, providing a perfect link path to generate flux.
Based on the winding arrangement
- Autotransformer: It will have a single winding wound on a laminated core. The primary and secondary share the same coil. Auto means "oneself" in the Greek language.
Based on the installation location
- Power Transformer – Used in power generating stations as they are suitable for high voltage applications.
- Distribution transformer: It is mainly used in distribution lines for domestic purposes. They are designed to carry low voltages. It is very easy to install and is characterized by low magnetic losses.
- Instrument transformers: They are mainly used to measure voltage, current, and power.
- Protection Transformers: They are used for the protection of components. In circuits, some components must be protected against voltage fluctuations, etc. The protection transformers ensure the protection of the components.
Working Principle of Transformer
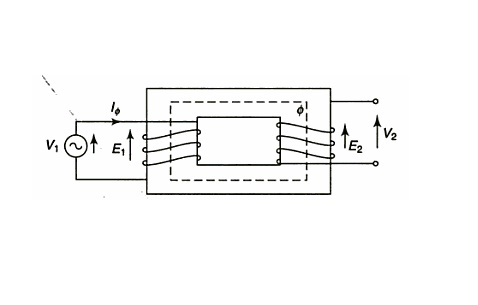
When alternating voltage V1 is applied to the primary winding of a transformer a current (termed as exciting current, IΦ) flows through it. The exciting current produces an alternating flux (Φ) in the core, which links with both the winding (primary and secondary). According to Faraday's laws of electromagnetic induction, the flux will cause self-induced emf E1 in the primary and mutually induced emf E2 in the secondary winding. But according to Lenz's law primary induced emf will oppose the applied voltage and in magnitude, this primary induced emf is (almost) equal to the applied voltage. Therefore, in brief, we can say emf induced in the primary winding is equal and opposite to the applied voltage.
When a load is connected to the secondary side, the current will start flowing in the secondary winding. The voltage induced in the secondary winding is responsible to deliver power to the load connected to it. In this way, power is transferred from one circuit (primary) to another (secondary) by winding through a magnetic circuit by electromagnetic induction. This is the working principle of the transformer. The induced emf in the secondary E2 is also in phase opposition to the applied voltage V1 at primary. if the secondary is open-circuited, terminal voltage V2 at the secondary is equal in magnitude and in phase with the induced emf at the secondary.
If N1 be the primary number of turns, then the RMS values of induced voltage at primary is given by-
E1 = 4.44 Φmax f N1
(As the induced voltage in the primary winding is equal and opposite to the applied voltage, so V1 = 4.44 Φmax f N1 ).
Similarly, the RMS value of the induced emf at secondary is obtained as
E2 = 4.44 Φmaxf N2
Thus for a single-phase ideal transformer, the expressions for the induced voltages at the primary as well as at the secondary windings can be obtained from the above Eqns.
You May Also Like-
EMF Equation of Transformer
Since the applied voltage is sinusoidal at the primary, the flux produced by the exciting current is also sinusoidal.If N1 be the primary number of turns, then the RMS values of induced voltage at primary is given by-
E1 = 4.44 Φmax f N1
(As the induced voltage in the primary winding is equal and opposite to the applied voltage, so V1 = 4.44 Φmax f N1 ).
Similarly, the RMS value of the induced emf at secondary is obtained as
E2 = 4.44 Φmaxf N2
Thus for a single-phase ideal transformer, the expressions for the induced voltages at the primary as well as at the secondary windings can be obtained from the above Eqns.





0 comments:
Post a Comment