(a)10^7
(b)10^5
(c)10^-4
(d)10^-6
Ans = a
8. Resistance of a copper wire always increases if
(a) temperature is reduced.
(b) temperature is increased.
(c) the number of free electrons available becomes less.
(d)the number of free electrons available becomes more.
Ans = b/c
9. Pure metals generally have
(a) high conductivity and low-temperature coefficient.
(b) high conductivity and large-temperature coefficient.
(c) low conductivity and zero temperature coefficient.
(d) low conductivity and high-temperature coefficient.
Ans = b
10. The temperature coefficient of resistance of a wire is 0.0008 °C, and the resistance of the wire is 8 ohm at 0°C, what is the resistance at 100°C?
(a) 8.64 Ohm.
(b) 8.08 Ohm.
(c) 7.92 Ohm.
(d) 7.20 Ohm.
Ans = a
11. If the length of a wire of resistance R is uniformly stretched to n times its original value, its new resistance is
(a) nR
(b) R/n
(c)n^2R
(d)R/n^2
n^2 = n square
Ans = c
12. The hot resistance of the filament of a bulb is higher than the cold resistance because the temperature coefficient of the filament is
(a) negative
(b) infinite
(c) zero
(d) positive
Ans = d
13. temperature coefficient of resistance of an insulator is
(a) positive and independent of temperature.
(b) negative and independent of temperature.
(c) negative and dependent on temperature.
(d) positive and dependent on temperature.
Ans = c
14. Four resistances 80 ohms,50 ohms,25 ohms, and R ohms are connected in parallel. Current through 25 ohms resistance is 4 A. The total current of the supply is 10 A. The value of R will be
(a) 66.66 ohm
(b) 40.25 ohm
(c) 36.36 ohm
(d) 76.56 ohm
Ans = c
15. Three parallel resistive branches are connected across a dc supply. What will be the ratio of the branch currents I1 :I2: I3, if the branch resistances are in the ratio R1: R2: R3:: 2: 4: 6?
(a) 3:2:6
(b) 2:4:6
(c) 6:3:2
(d) 6:2:4
Ans = c
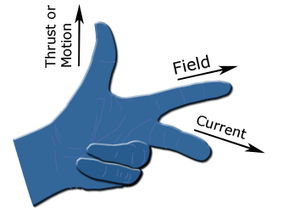
16. The flow of electric current in a conductor is due to the flow of
(a) electrons
(b) protons
(c) electrons and ions
(d) charged particles
Ans = a
17. An electric current is the
(a) the random movement of electrons in a conductor
(b) movement of free electrons predominately in one direction
(c) the pressure difference between two poles
(d) the power that causes drifts of electrons
Ans = b
18. How are 500-ohm resisters connected so as to give an effective resistance of 750 ohm?
(a) three resistors of 500 ohms each, in parallel
(b) three resistors of 500 ohms each, in series
(c) two resistors of 500 ohms each, in parallel
(d) two resistors of 500 ohms each, in parallel, and the combination in series with another 500-ohm resister.
Ans = d
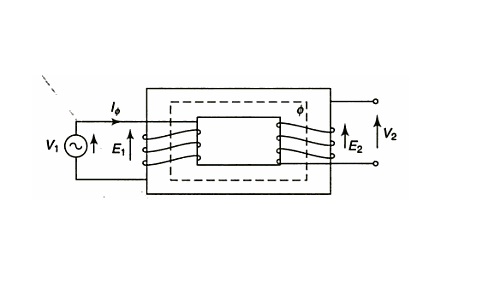
19. When an electric current flows through a conductor, its temperature rises. This is because of
(a) mutual collisions between metal atoms.
(b) mutual collisions between conducting elections.
(c) collisions between conduction electrons and atoms.
(d) release of conduction electrons from parent atoms.
Ans = c
20. Two heaters, rated at 1000 W, 250 V each are connected in series across a 250 V, 50 Hz ac mains. The total power drawn from the supply would be _____W.
(a) 1,000
(b) 500
(c) 250
(d) 2,000
Ans = b
21. Four 100 W bulbs are connected in parallel across a 200 V supply line. If one bulb gets fused
(a) no bulb will light.
(b) all four bulbs will light.
(c) rest of the three bulbs will light.
(d) none of the above.
Ans = c
22. A 200 W, 230 V lamp is connected across a 115 V supply. The lamp will draw power
(a) slightly more than 50 W.
(b) slightly less than 50 W.
(c) exactly 100 W.
(d) exactly 50 W.
Ans = a
23. Two incandescent light bulbs of 40 W and 60 W ratings are connected in series across the mains. Then
(a) the bulbs together consume 100 W.
(b) the bulbs together consume 50 W.
(c) the 60 W bulb glows brighter.
(d) the 40 W bulb glows brighter.
Ans = d
24. A 100-watt light bulb burns on an average of 10 hours a day for one week. The Weekly consumption of energy will be ___unit/s.
(a) 7
(b) 70
(c) 0.7
(d) 0.07
Ans = a
25. Which of the following statements is incorrect?
(a) Resistance is a passive element.
(b) Inductor is a passive element.
(c) Current source is a passive element.
(d) Voltage source is an active element.
26. The terminals across the source are ____ if a current source is to be neglected.
(a) open-circuited
(b) short-circuited
(c) replaced by a capacitor
(d) replaced by a source resistance
Ans = a
27. Which of the following is an active element in a circuit?
(a) Current source.
(b) Resistance.
(c) Inductance.
(d) Capacitance.
Ans = a
28. Which of the following is not a bilateral element?
(a) Constant current source.
(b) Resistor.
(c) Inductor.
(d) Capacitor.
29. A circuit having the same properties in either direction is known as ____ circuit.
(a) bilateral
(c) irreversible
(b) unilateral
(d) reversible
Ans = a
30. The elements which are not capable of delivering energy on their own are known as
(a) unilateral elements.
(b) nonlinear elements.
(c) passive elements.
(d) active elements.
Ans = c
Read -